1. Introduction

The Union-Find (Disjoint Set Union, DSU) algorithm is used to efficiently keep track of a partition of a set into disjoint subsets. It has two main operations:

  • Union: Merge two subsets.
  • Find: Determine which particular subset the element belongs.

2. Operations

2.1 Find Operation

Keep traveling towards the parent until we reach the top (no more parent). 2-1

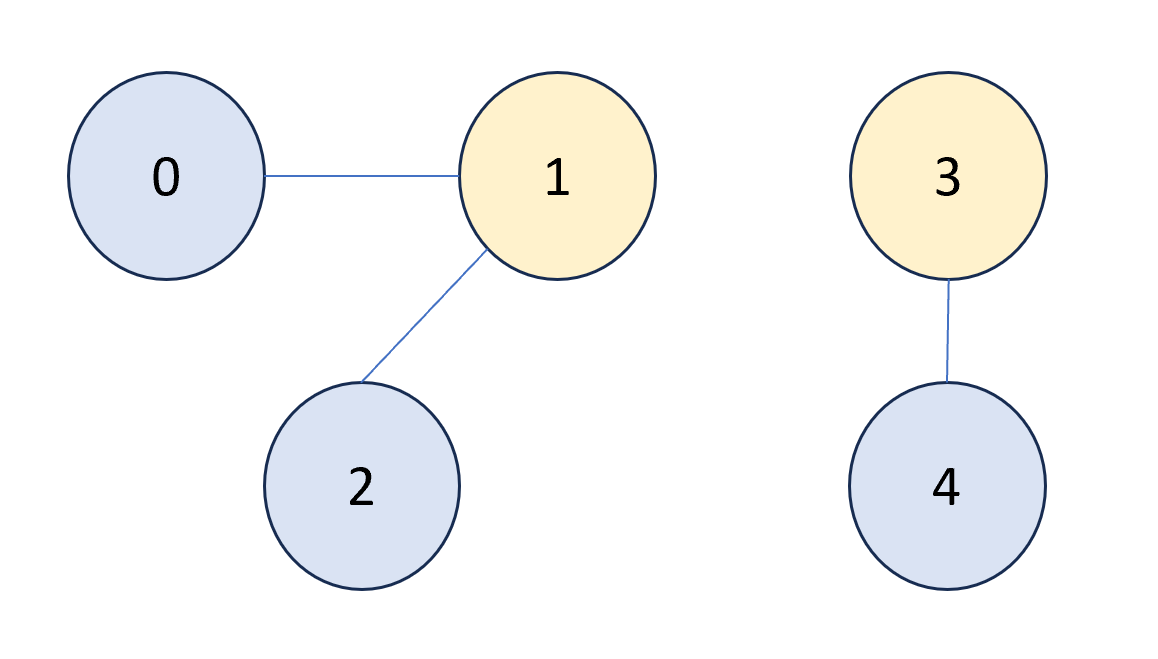
  • Let 1 represent the parent of left group and 3 represents the parent of right group.
    parent = [1, 1, 1, 3, 3] at this point.
  • Call find(x), x = 2:
    • parent[2] = 1 and 1 != x then keep traveling x = parent[x] = 1
    • parent[1] = 1 and 1 == x then stop

2.2 Union Operation

Merge y subset into x subset by assigning x’s parent to y. 2-2

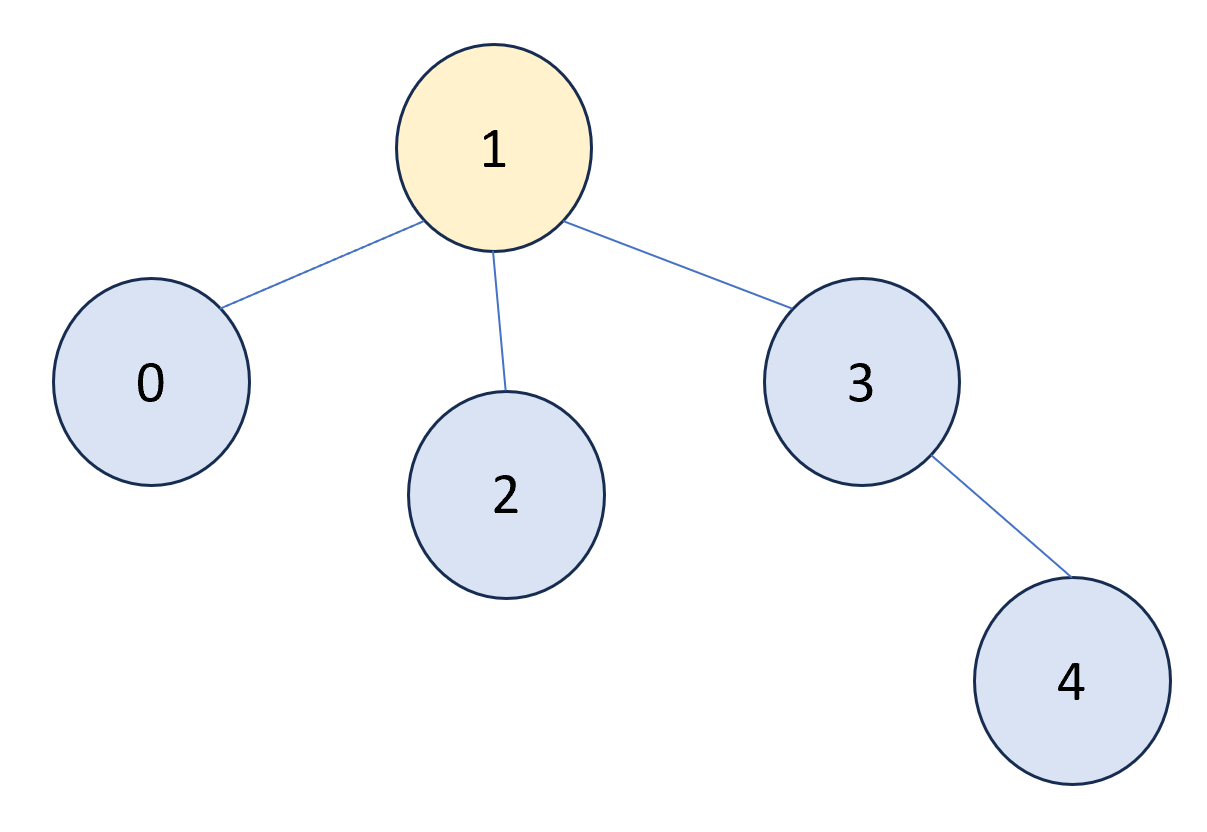
  • Call union(2, 3):
    • Assign 3’s parent as 2’s parent. parent = [1, 1, 1, 1, 3] at this point.
class UnionFind(object):
	#Initialize with parent[i] = i
	def __init__(self, n):
		self.parent = range(n)
	
	#recursively find element's parent until its parent equal to itself (no parent)
	def find(self, x):
		return self.find(self.parent[x]) if self.parent[x] != x else x
	
	#merge y's subset into x's subset
	def union(self, x, y):
		self.parent[self.find(y)] = self.find(x)

3 Union Find Algorithms for Set Partition

Suppose we want to find the number of subsets in the following graph. 3-1

\[Adj = [\begin{bmatrix}1 & 1 & 1 & 0 & 0\end{bmatrix} \\ \begin{bmatrix}1 & 1 & 1 & 0 & 0\end{bmatrix} \\ \begin{bmatrix}1 & 1 & 1 & 0 & 0\end{bmatrix} \\ \begin{bmatrix}0 & 0 & 0 & 1 & 1\end{bmatrix} \\ \begin{bmatrix}0 & 0 & 0 & 1 & 1\end{bmatrix}]\]

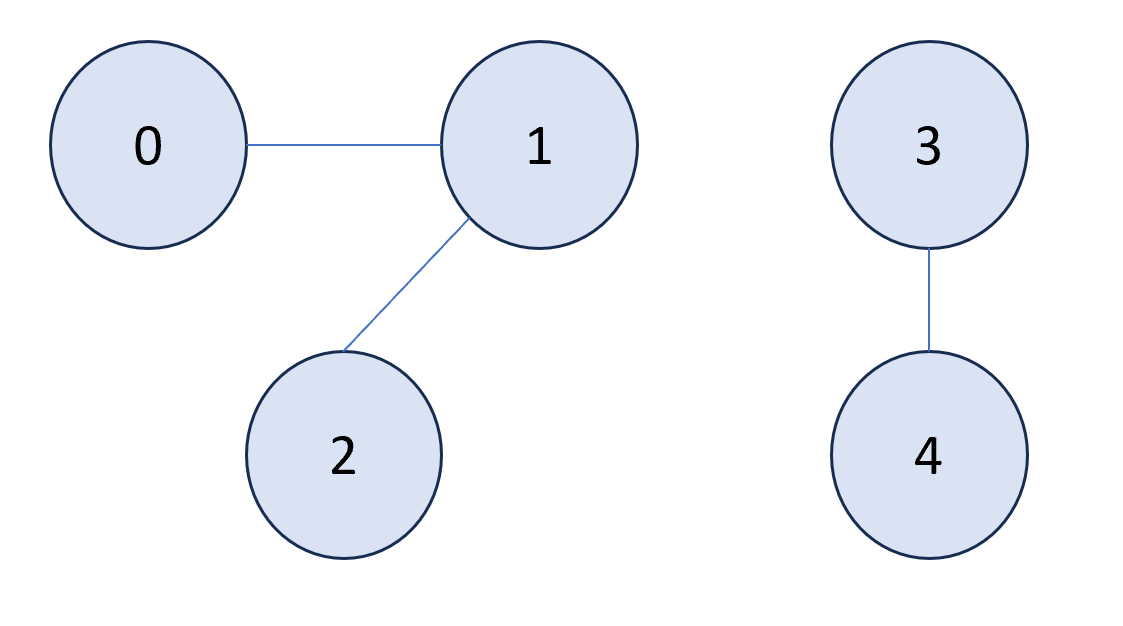
1. Initialize with parent[i] = i. 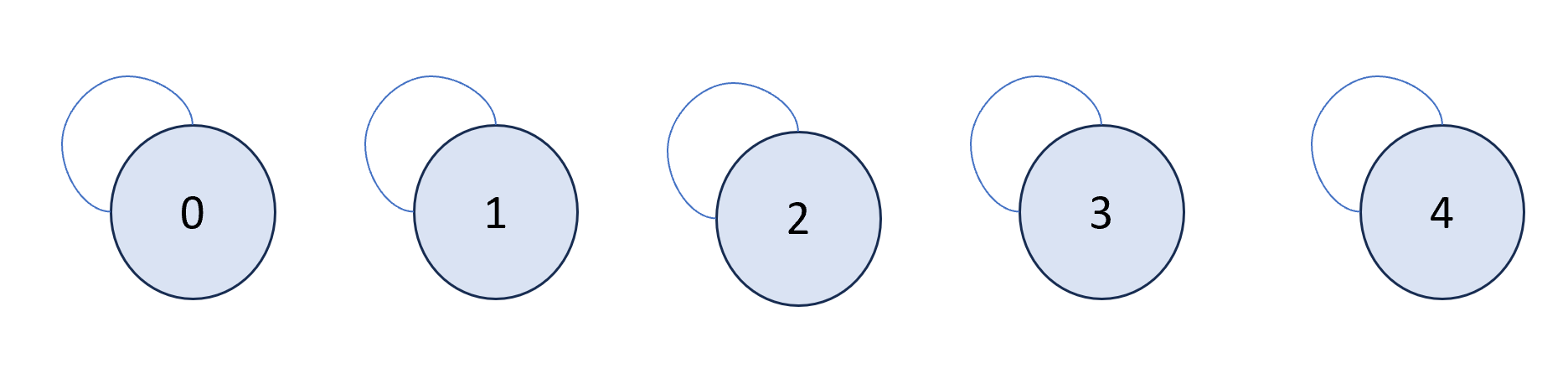3-2 \(parent = \begin{bmatrix}0 & 1 & 2 & 3 & 4 \end{bmatrix}\)

2. Loop through each node to decide whether call union based on connectivity.

  • node = 0: 1 and 2 are connected, so call union(0, 1) and union(0, 2) 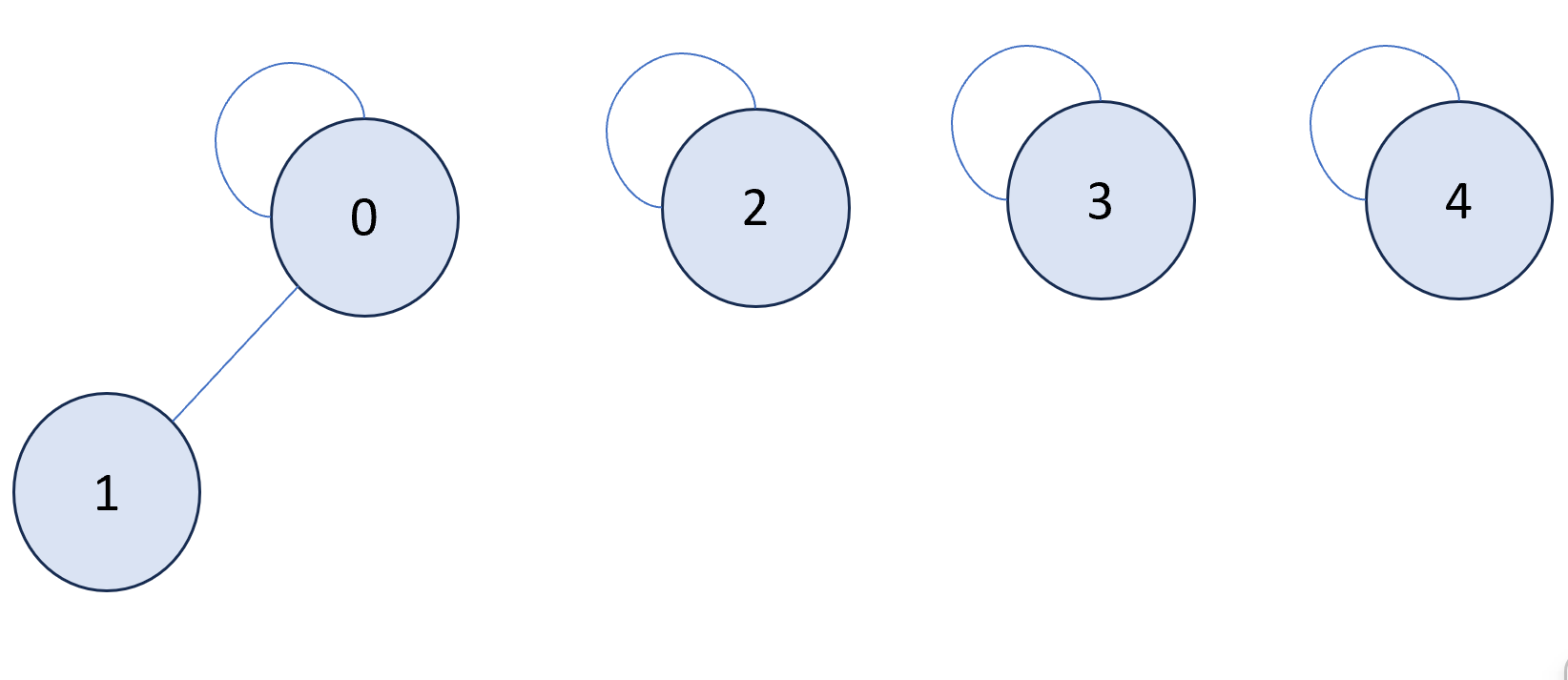3-3 \(parent = \begin{bmatrix}0 & 0 & 2 & 3 & 4 \end{bmatrix}\) 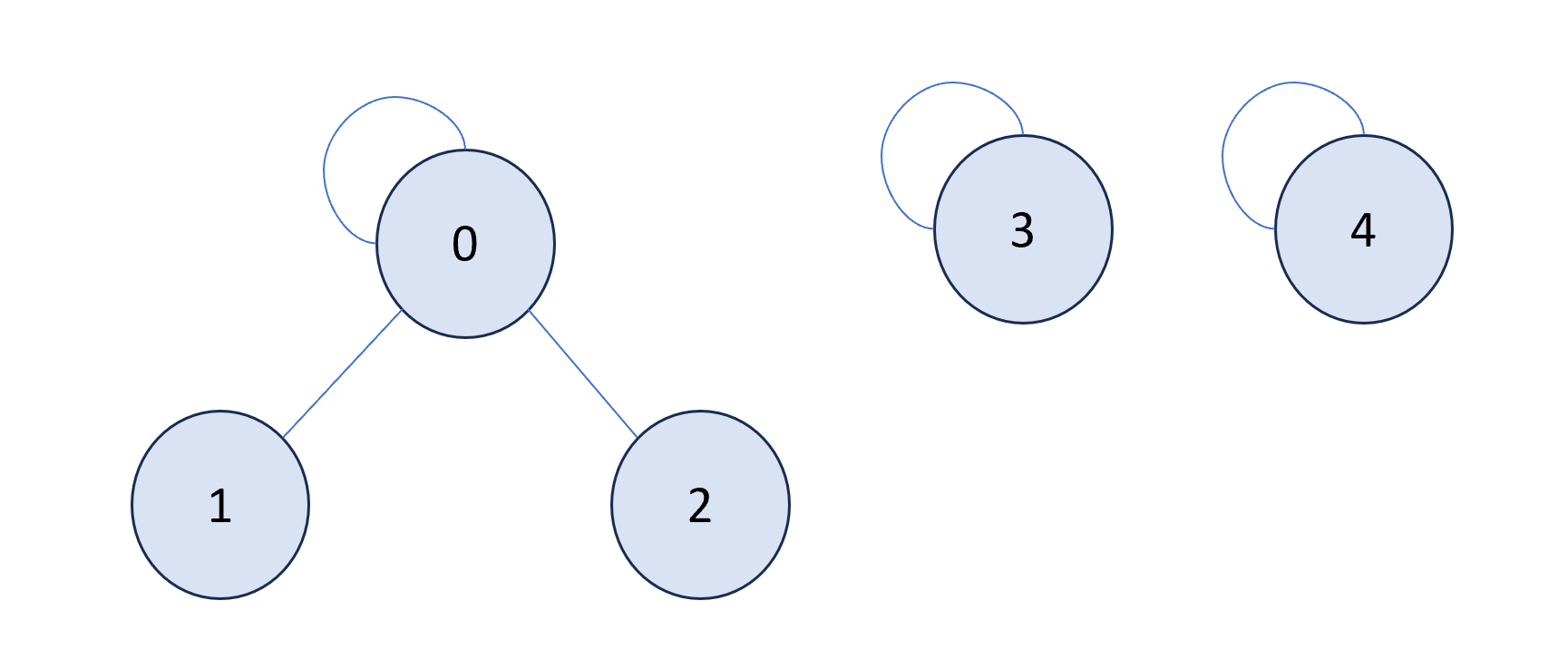3-4 \(parent = \begin{bmatrix}0 & 0 & 0 & 3 & 4 \end{bmatrix}\)

  • node = 1: 0 and 2 are connected, so call union(1, 0) and union(1, 2) -> graph remains the same
  • node = 2: 0 and 1 are connected, so call union(2, 0) and union(2, 1) -> graph remains the same
  • node = 3: 4 is connected, so call union(3, 4) 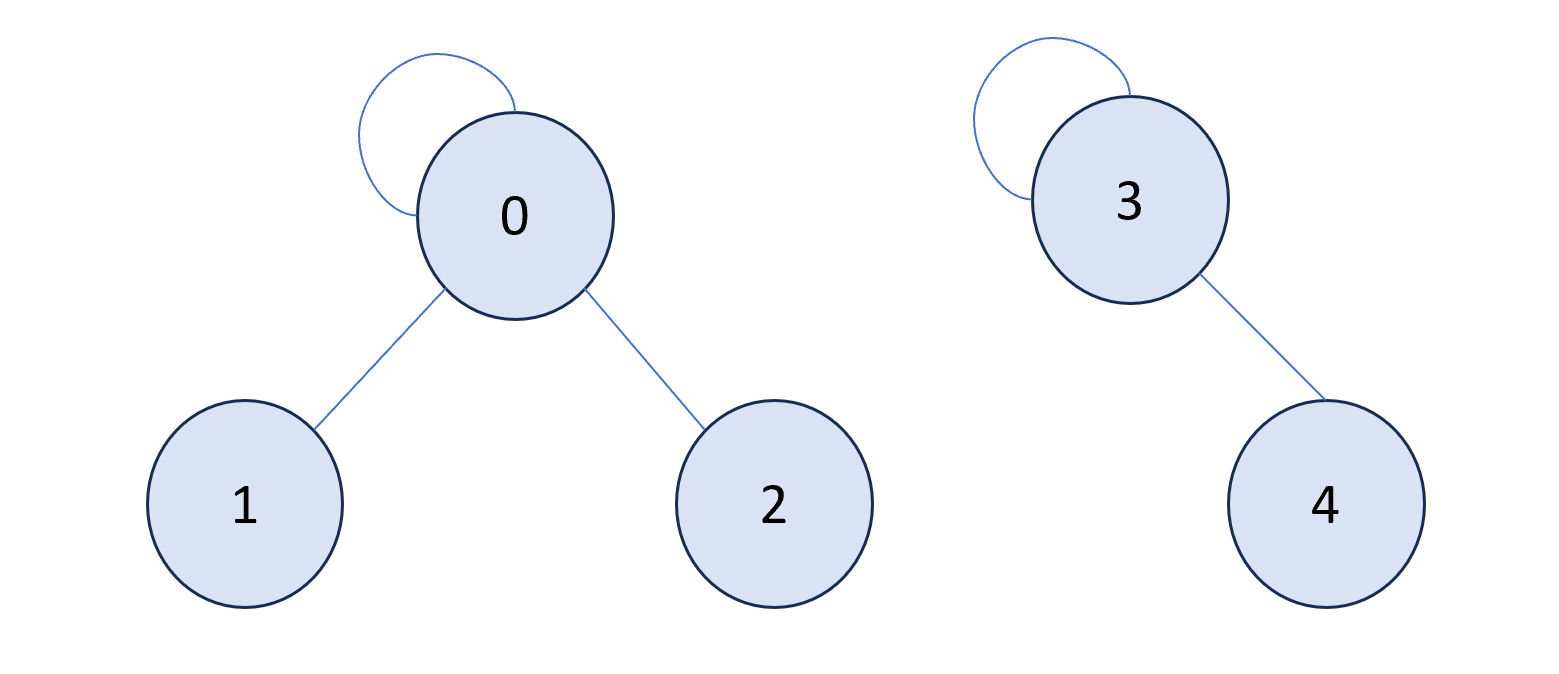3-4 \(parent = \begin{bmatrix}0 & 0 & 0 & 3 & 3 \end{bmatrix}\)
  • node = 4: 3 is connected, call union(4, 3) and union(2, 1) -> graph remains the same

3. Loop through parent array via find function to see which subset the node belongs to.

def FindSubsetNum(object):
	n = len(Adj)
	uf = UnionFind(n)
	for node_1, row_arr in enumerate(Adj):
		for node_2, connection in enumerate(row_arr):
			if connection == 1:
				uf.union(node_1, node_2)

	return len(set([uf.find(node) for node in uf.parent]))